–§–æ—Ä—É–º –Ý–∞–¥–∏–æ–ö–æ—Ç • –ü—Ä–æ—Å–º–æ—Ç—Ä —Ç–µ–º—ã - FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–°–æ–æ–±—â–µ–Ω–∏—è –±–µ–∑ –æ—Ç–≤–µ—Ç–æ–≤ | –ê–∫—Ç–∏–≤–Ω—ã–µ —Ç–µ–º—ã
–°—Ç—Ä–∞–Ω–∏—Ü–∞ 6 –∏–∑ 10
[ –°–æ–æ–±—â–µ–Ω–∏–π: 200 ]
... , , , , , , ,
–ê–≤—Ç–æ—Ä
–°–æ–æ–±—â–µ–Ω–∏–µ
ARV
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–î–æ–±–∞–≤–ª–µ–Ω–æ: –í—Å –∞–ø—Ä 05, 2015 08:08:32
–£–º, —á–µ—Å—Ç—å –∏ —Å–æ–≤–µ—Å—Ç—å. –ò —Å–∫—Ä–æ–º–Ω–æ—Å—Ç—å.
–ö–∞—Ä–º–∞: 98
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 2135
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç –¥–µ–∫ 28, 2006 08:19:56–°–æ–æ–±—â–µ–Ω–∏–π: 18446–û—Ç–∫—É–¥–∞: –ù–æ–≤–æ—á–µ—Ä–∫–∞—Å—Å–∫
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
–ú–µ–¥–∞–ª–∏: 2
–º–æ–∂–Ω–æ –∑–∞–ª–∏—Ç—å –Ω–∞ yputube –∏ —Ä–∞–∑–º–µ—Å—Ç–∏—Ç—å –∑–¥–µ—Å—å...
–µ—Å–ª–∏ —Ä–∞—Å—Å–º–∞—Ç—Ä–∏–≤–∞—Ç—å —á–µ–ª–æ–≤–µ–∫–∞ —Å–Ω–∏–∑—É, –ø–æ–∫–∞–∂–µ—Ç—Å—è, —á—Ç–æ –º–æ–∑–≥ —É –Ω–µ–≥–æ –≥–ª—É–±–æ–∫–æ –≤ –∂–æ–ø–µ–ú–æ–π —É—é—Ç–Ω—ã–π –±–ª–æ–∂–∏–∫ ... –∑–∞—Ö–æ–¥–∏—Ç–µ!
–í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö
–Ý–µ–∫–ª–∞–º–∞
YS
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–î–æ–±–∞–≤–ª–µ–Ω–æ: –í—Å –∞–ø—Ä 05, 2015 09:17:17
–î—Ä—É–≥ –ö–æ—Ç–∞
–ö–∞—Ä–º–∞: 77
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 1247
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –í—Å –º–∞—Ä 29, 2009 22:09:05–°–æ–æ–±—â–µ–Ω–∏–π: 7518
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
–¶–∏—Ç–∞—Ç–∞:
–ü–µ—Ä—Å–æ–Ω–∞–ª—å–Ω–æ–µ —Å–ø–∞—Å–∏–±–æ YS –∑–∞ —Å–ø–æ–∫–æ–π–Ω—ã–π –∏ –≤—Ä–∞–∑—É–º–∏—Ç–µ–ª—å–Ω—ã–π –ª–∏–∫–±–µ–∑!
–ù–µ –∑–∞ —á—Ç–æ, –Ω–µ –∑–∞ —á—Ç–æ.
–°–ø–æ–∫–æ–π—Å—Ç–≤–∏–µ - –æ–¥–Ω–∞ –∏–∑ –∫–æ–Ω—Ñ—É—Ü–∏–∞–Ω—Å–∫–∏—Ö –¥–æ–±—Ä–æ–¥–µ—Ç–µ–ª–µ–π.
–ü–æ –ø—É—Ç–∏ —è –∏ —Å–∞–º –≤–æ –º–Ω–æ–≥–æ–º —Ä–∞–∑–æ–±—Ä–∞–ª—Å—è, –∏–±–æ —Ç–æ–∂–µ –ø—Ä–∏—à–ª–æ—Å—å –ø–æ–¥—É–º–∞—Ç—å.
–í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö
–Ý–µ–∫–ª–∞–º–∞
zenek
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–î–æ–±–∞–≤–ª–µ–Ω–æ: –í—Ç –∞–≤–≥ 11, 2015 14:35:31
–ö–∞—Ä–º–∞: 1
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 0
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –°—Ä –∞–ø—Ä 28, 2010 17:49:14–°–æ–æ–±—â–µ–Ω–∏–π: 116
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
–ó–¥—Ä–∞–≤—Å—Ç–≤—É–π—Ç–µ!
–ï—Å—Ç—å —Å–∏–≥–Ω–∞–ª –∫–æ—Ç–æ—Ä—ã–π –ø–æ–¥–≤–µ—Ä–≥–∞–µ—Ç—Å—è –¥–∏—Å–∫—Ä–µ—Ç–Ω–æ–º—É –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏—é —Ñ—É—Ä—å–µ.
–ù–∞ –≤—ã—Ö–æ–¥–µ –î–ü–§ –µ—Å—Ç—å –º–Ω–∏–º–∞—è –∏ –¥–µ–π—Å—Ç–≤–∏—Ç–µ–ª—å–Ω–∞—è —á–∞—Å—Ç–∏, –∫–æ—Ä–µ–Ω—å –∏–∑ —Å—É–º–º—ã –∫–≤–∞–¥—Ä–∞—Ç–æ–≤ –∫–æ—Ç–æ—Ä—ã—Ö –µ—Å—Ç—å –∞–º–ø–ª–∏—Ç—É–¥–∞ –æ–ø—Ä–µ–¥–µ–ª–µ–Ω–Ω–æ–π —á–∞—Å—Ç–æ—Ç—ã –≤ —Å–∏–≥–Ω–∞–ª–µ.
–í–æ—Ç –Ω–∞–ø–∏—Å–∞–ª –Ω–µ–±–æ–ª—å—à—É—é –ø—Ä–æ–≥—Ä–∞–º–º–∫—É, –∫–æ—Ç–æ—Ä–∞—è –≥–µ–Ω–µ—Ä–∏—Ä—É–µ—Ç —Å–∏–≥–Ω–∞–ª –∏ –ø—Ä–æ–≤–æ–¥–∏—Ç –Ω–∞–¥ –Ω–∏–º –ø—Ä—è–º–æ–µ –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏–µ —Ñ—É—Ä—å–µ:
–ö–æ–¥:
#include "stdafx.h"
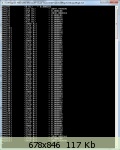
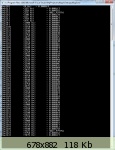
–í–æ—Ç —Ä–µ–∑—É–ª—å—Ç–∞—Ç —Ä–∞–±–æ—Ç—ã –ø—Ä–æ–≥—Ä–∞–º–º—ã –¥–ª—è —Å–∏–≥–Ω–∞–ª–∞ - —Å–∏–Ω—É—Å 125–ì—Ü + —Å–∏–Ω—É—Å 375–ì—Ü:
–ê –≤–æ—Ç –¥–ª—è –ø—Ä–æ—Å—Ç–æ —Å–∏–Ω—É—Å–∞ 375–ì—Ü:
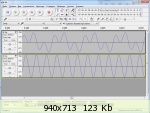
–î–ª—è –ø–æ–Ω–∏–º–∞–Ω–∏—è, –≤–æ—Ç —Å–∞–º–∏ —Å–∏–≥–Ω–∞–ª—ã:
–ß–∞—Å—Ç–æ—Ç–∞ –¥–∏—Å–∫—Ä–µ—Ç–∏–∑–∞—Ü–∏–∏ —Å–∏–≥–Ω–∞–ª–∞ - 8000–ì—Ü.
–¢–µ–ø–µ—Ä—å –≤–æ–ø—Ä–æ—Å!
–ö–∞–∫ –æ–ø—Ä–µ–¥–µ–ª–∏—Ç—å —Ä–µ–∞–ª—å–Ω—É—é –∞–º–ø–ª–∏—Ç—É–¥—É? –í —Ä–µ–∑—É–ª—å—Ç–∞—Ç–∞—Ö —Ä–∞–±–æ—Ç—ã –ø—Ä–æ–≥—Ä–∞–º–º—ã –∞–º–ø–ª–∏—Ç—É–¥–∞ –ø–ª—è—à–µ—Ç –¥–ª—è –¥–≤—É—Ö —Å–∏–Ω—É—Å–æ–≤ - –ø–æ 2048 –Ω–∞ —á–∞—Å—Ç–æ—Ç—É, –¥–ª—è –æ–¥–Ω–æ–≥–æ —Å–∏–Ω—É—Å–∞ - 4064 –µ–¥–∏–Ω–∏—Ü. –ß—Ç–æ —ç—Ç–æ –∑–∞ –µ–¥–∏–Ω–∏—Ü—ã? –ö–∞–∫ –∏–∑ –ø—Ä–∏–≤–µ—Å—Ç–∏ –∫ –Ω–æ—Ä–º–∞–ª—å–Ω–æ–º—É –≤–∏–¥—É? –ò –∫–∞–∫ –∏–∑ –Ω–∏—Ö –ø–æ–ª—É—á–∏—Ç—å –≤ –¥–±, –∫–∞–∫–æ–µ –∑–Ω–∞—á–µ–Ω–∏–µ –ø—Ä–∏–Ω–∏–º–∞—Ç—å –∑–∞ 0–î–±?
–í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö
WiseLord
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–î–æ–±–∞–≤–ª–µ–Ω–æ: –í—Ç –∞–≤–≥ 11, 2015 15:18:08
–î—Ä—É–≥ –ö–æ—Ç–∞
–ö–∞—Ä–º–∞: 86
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 1035
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç –∞–ø—Ä 11, 2013 11:19:59–°–æ–æ–±—â–µ–Ω–∏–π: 4895–û—Ç–∫—É–¥–∞: –ú–∏–Ω—Å–∫
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
–¶–∏—Ç–∞—Ç–∞:
–ö–æ–¥:
for(i=0; i<DFT_SIZE; i++) {
–¶–∏–∫–ª 64 —Ä–∞–∑–∞ –ø–æ 64 —Ä–∞–∑–∞. –í–æ—Ç –∏ –≤—ã—Ö–æ–¥–∏—Ç, –µ—Å–ª–∏ —á–∞—Å—Ç–æ—Ç–∞ –æ–¥–Ω–∞ - –Ω–∞ –Ω–µ–π –∏ –≤—ã—Ö–æ–¥–∏—Ç –º–∞–∫—Å–∏–º—É–º (4096, –µ—Å–ª–∏ –±–µ–∑ –æ—à–∏–±–æ–∫ –æ–∫—Ä—É–≥–ª–µ–Ω–∏—è), –µ—Å–ª–∏ –∫–æ–º–±–∏–Ω–∞—Ü–∏—è —á–∞—Å—Ç–æ—Ç - —Å—É–º–º–∞—Ä–Ω–∞—è –∞–º–ø–ª–∏—Ç—É–¥–∞ —Ç–æ–∂–µ –±—É–¥–µ—Ç —Ç–∞–∫–æ–π.
–¢–∞–∫ —á—Ç–æ –Ω–∞–¥–æ —Ä–µ–∑—É–ª—å—Ç–∞—Ç (–∏ –¥–µ–π—Å—Ç–≤–∏—Ç–µ–ª—å–Ω—É—é —á–∞—Å—Ç—å, –∏ –º–Ω–∏–º—É—é) –Ω–∞ DFT_SIZE —Ä–∞–∑–¥–µ–ª–∏—Ç—å, —á—Ç–æ–±—ã –ø–æ–ª—É—á–∏—Ç—å –∞–º–ø–ª–∏—Ç—É–¥—ã –≤ —Ç–µ—Ö –∂–µ "–ø–æ–ø—É–≥–∞—è—Ö", –≤ –∫–æ—Ç–æ—Ä—ã—Ö –±—ã–ª–∏ –∏—Å—Ö–æ–¥–Ω—ã–µ —Å–∏–≥–Ω–∞–ª—ã.
–í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö
–Ý–µ–∫–ª–∞–º–∞
YS
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–î–æ–±–∞–≤–ª–µ–Ω–æ: –í—Ç –∞–≤–≥ 11, 2015 16:33:45
–î—Ä—É–≥ –ö–æ—Ç–∞
–ö–∞—Ä–º–∞: 77
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 1247
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –í—Å –º–∞—Ä 29, 2009 22:09:05–°–æ–æ–±—â–µ–Ω–∏–π: 7518
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
zenek , –≤–∞—à –ª–∏—Å—Ç–∏–Ω–≥ - –Ω–∞–≥–ª—è–¥–Ω–∞—è –¥–µ–º–æ–Ω—Å—Ç—Ä–∞—Ü–∏—è —Ç–æ–≥–æ, –ø–æ—á–µ–º—É —è –≤—Å–µ–≥–¥–∞ –≤—Å–µ–º —Å–æ–≤–µ—Ç—É—é –ø–∏—Å–∞—Ç—å –∫–æ–º–º–µ–Ω—Ç–∞—Ä–∏–∏ —Ç–æ–ª—å–∫–æ –Ω–∞ –∞–Ω–≥–ª–∏–π—Å–∫–æ–º.
–í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö
–Ý–µ–∫–ª–∞–º–∞
INA
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–î–æ–±–∞–≤–ª–µ–Ω–æ: –ß—Ç —è–Ω–≤ 14, 2016 21:27:45
–ü–µ—Ä–≤—ã–π —Ä–∞–∑ —Å–∫–∞–∑–∞–ª –ú—è—É!
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ü–Ω –º–∞—Ä 23, 2015 17:18:47–°–æ–æ–±—â–µ–Ω–∏–π: 27
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
–î–æ–±—Ä—ã–π –≤–µ—á–µ—Ä –≤—Å–µ–º!
–ü—Ä–æ–¥–æ–ª–∂–∏–≤ —Ç–µ–º—É –ø—Ä–æ FFT, –Ω–∞–ø–∏—Å–∞–ª –Ω–µ–±–æ–ª—å—à—É—é —Å–æ—Ñ—Ç–∏–Ω–∫—É –ø–æ–¥ Android...
–í–æ—Ç —Ç–æ, —á—Ç–æ –ø–æ–ª—É—á–∏–ª–æ—Å—å:
https://youtu.be/eDiQ7_FXkuk –≠—Ç–æ –Ω–µ–º–Ω–æ–∂–∫–æ –Ω–µ –≤ —ç—Ç—É —Ç–µ–º—É —Ñ–æ—Ä—É–º–∞... –Ω–∞–¥–µ—é—Å—å, –º–µ–Ω—è –ø—Ä–æ—Å—Ç—è—Ç...
P.S. –ê —ç—Ç–æ:
https://youtu.be/WyIumlJ8TME —Ç–æ, —á—Ç–æ –±—ã–ª–æ —Å–¥–µ–ª–∞–Ω–æ —Ä–∞–Ω—å—à–µ –Ω–∞ ATMega32...
–í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö
–Ý–µ–∫–ª–∞–º–∞
INA
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–î–æ–±–∞–≤–ª–µ–Ω–æ: –°—Ä —è–Ω–≤ 20, 2016 16:52:54
–ü–µ—Ä–≤—ã–π —Ä–∞–∑ —Å–∫–∞–∑–∞–ª –ú—è—É!
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ü–Ω –º–∞—Ä 23, 2015 17:18:47–°–æ–æ–±—â–µ–Ω–∏–π: 27
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
–í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö
Rtmip
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–î–æ–±–∞–≤–ª–µ–Ω–æ: –ß—Ç —è–Ω–≤ 21, 2016 08:38:58
–î–µ—Ä–∂–∏—Ç –ø–∞—è–ª—å–Ω–∏–∫ —Ö–≤–æ—Å—Ç–æ–º
–ö–∞—Ä–º–∞: 10
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 161
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç –∞–ø—Ä 03, 2014 23:16:55–°–æ–æ–±—â–µ–Ω–∏–π: 963–û—Ç–∫—É–¥–∞: –Ý–æ—Å—Å–∏—è
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
INA –ø–∏—Å–∞–ª(–∞):
–î–æ–±—Ä—ã–π –≤–µ—á–µ—Ä –≤—Å–µ–º!
–ü—Ä–æ–¥–æ–ª–∂–∏–≤ —Ç–µ–º—É –ø—Ä–æ FFT, –Ω–∞–ø–∏—Å–∞–ª –Ω–µ–±–æ–ª—å—à—É—é —Å–æ—Ñ—Ç–∏–Ω–∫—É –ø–æ–¥ Android...
–í–æ—Ç —Ç–æ, —á—Ç–æ –ø–æ–ª—É—á–∏–ª–æ—Å—å:
https://youtu.be/eDiQ7_FXkuk –≠—Ç–æ –Ω–µ–º–Ω–æ–∂–∫–æ –Ω–µ –≤ —ç—Ç—É —Ç–µ–º—É —Ñ–æ—Ä—É–º–∞... –Ω–∞–¥–µ—é—Å—å, –º–µ–Ω—è –ø—Ä–æ—Å—Ç—è—Ç...
–ò–≥–æ—Ä—å –ù–∏–∫–æ–ª–∞–µ–≤–∏—á, —è –ø—Ä–æ—Å—Ç–∏–ª, –¥–∞!
–ù–æ –≥–¥–µ –∂–µ –æ–Ω–∞?
"–°–æ—Ñ—Ç–∏–Ω–∫–∞" –≥–¥–µ? –ò–Ω—Ç–µ—Ä–µ—Å–Ω–æ –ø–æ–ø—Ä–æ–±–æ–≤–∞—Ç—å.
–í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö
INA
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–î–æ–±–∞–≤–ª–µ–Ω–æ: –ß—Ç —è–Ω–≤ 21, 2016 21:43:13
–ü–µ—Ä–≤—ã–π —Ä–∞–∑ —Å–∫–∞–∑–∞–ª –ú—è—É!
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ü–Ω –º–∞—Ä 23, 2015 17:18:47–°–æ–æ–±—â–µ–Ω–∏–π: 27
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
–î–æ–±—Ä–æ–π –Ω–æ—á–∏!
–í–ª–æ–∂–µ–Ω–∏—è:
Spectre.rar [483.74 KiB]
–°–∫–∞—á–∏–≤–∞–Ω–∏–π: 226
–í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö
–Ý–µ–∫–ª–∞–º–∞
Ypir
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–î–æ–±–∞–≤–ª–µ–Ω–æ: –í—Ç –¥–µ–∫ 06, 2016 17:14:43
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ü–Ω –∏—é–ª 21, 2014 21:08:02–°–æ–æ–±—â–µ–Ω–∏–π: 1
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
–î–æ–±—Ä—ã–π –≤–µ—á–µ—Ä! –ü–æ–ø—Ä–æ–±–æ–≤–∞–ª —Ä–µ–∞–ª–∏–∑–æ–≤–∞—Ç—å FFT, –Ω–æ –≤–æ–∑–Ω–∏–∫–ª–æ –Ω–µ—Å–∫–æ–ª—å–∫–æ –≤–æ–ø—Ä–æ—Å–æ–≤.
–í–æ–ø—Ä–æ—Å 1: –ü—Ä–∏ –ø–æ–ª—É—á–µ–Ω–∏–∏ —Å–ø–µ–∫—Ç—Ä–∞ —Ä–µ–∑—É–ª—å—Ç–∞—Ç –Ω–∞–ø–æ–º–∏–Ω–∞–µ—Ç –ø–∏–ª—É, —Ç.–µ. –ø–µ—Ä–µ–º–µ–Ω–Ω–∞—è am –Ω–∞—Ä–∞—Å—Ç–∞–µ—Ç –¥–æ 0xFF –∑–∞—Ç–µ–º –æ–±–Ω—É–ª—è–µ—Ç—å—Å—è –∏ —Å–Ω–æ–≤–∞ —Ä–∞—Å—Ç–µ—Ç, –¥–æ–ª–∂–Ω–æ –ª–∏ —Ç–∞–∫ –±—ã—Ç—å?
–ö–æ–¥:
{
–í–æ–ø—Ä–æ—Å 2: –ï—Å–ª–∏ —Ä–µ–∑—É–ª—å—Ç–∞—Ç –ø—Ä–µ–æ–±—Ä–∞–∑–æ–≤–∞–Ω–∏—è (–ø–µ—Ä–µ–º–µ–Ω–Ω–∞—è am) –∑–∞—Å—É–Ω—É—Ç—å –≤ —à–∏–º, –±–∞–Ω–∞–ª—å–Ω–æ OCR0A=am, –ø–æ–ª—É—á–∞–µ—Ç—Å—è —á—Ç–æ —Ç–æ –Ω–µ–ø–æ–Ω—è—Ç–Ω–æ–µ, —Å–æ–±—Å—Ç–≤–µ–Ω–Ω–æ –ø–æ–¥—Å–∫–∞–∂–∏—Ç–µ –ø–æ–∂–∞–ª—É–π—Å—Ç–∞ –∫–∞–∫ –æ–±—Ä–∞–±–æ—Ç–∞—Ç—å —Ä–µ–∑—É–ª—å—Ç–∞—Ç —á—Ç–æ –±—ã –∑–∞—Å—É–Ω—É—Ç—å –µ–≥–æ –≤ —à–∏–º –∏ —Å–∫–∞–∂–µ–º –ø–æ–º–∏–≥–∞—Ç—å –¥–∏–æ–¥–æ–º? –ö–∞–∫ —è –ø–æ–Ω–∏–º–∞—é —á–µ–º —á–∞—Å—Ç–æ—Ç–∞ –±–ª–∏–∂–µ –∫ –∏—Å–∫–æ–º–æ–π —Ç–µ–º —á–∞—â–µ –æ–Ω –¥–æ–ª–∂–µ–Ω –º–æ—Ä–≥–∞—Ç—å, –ø—Ä–∞–≤–¥–∞ —ç—Ç–æ –ø—Ä–∏ –Ω–µ–±–æ–ª—å—à–æ–π –æ—Ç—Å—Ç—Ä–æ–π–∫—É –ø–æ —á–∞—Å—Ç–æ—Ç–µ.
–í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö
NebelWefer
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–î–æ–±–∞–≤–ª–µ–Ω–æ: –ß—Ç —è–Ω–≤ 05, 2017 13:53:53
–ì—Ä—ã–∑–µ—Ç –∫–∞–Ω–∏—Ñ–æ–ª—å
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç –∞–ø—Ä 16, 2009 14:23:59–°–æ–æ–±—â–µ–Ω–∏–π: 274
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
–¢–æ–≤–∞—Ä–∏—â–∏, –ø—Ä–∞–≤–∏–ª—å–Ω–æ –ª–∏ —è –ø–æ–Ω—è–ª: –µ—Å–ª–∏ –º–Ω–µ –ø—Ä–∏ –∞–Ω–∞–ª–∏–∑–µ –∑–≤—É–∫–æ–≤–æ–≥–æ —Å–∏–≥–Ω–∞–ª–∞ –Ω–µ –∏–Ω—Ç–µ—Ä–µ—Å–Ω—ã —á–∞—Å—Ç–æ—Ç—ã –≤—ã—à–µ 15–∫–ì—Ü, —Ç–æ —è –º–æ–≥—É —Å–Ω–∏–∑–∏—Ç—å —á–∞—Å—Ç–æ—Ç—É –¥–∏—Å–∫—Ä–µ—Ç–∏–∑–∞—Ü–∏–∏ –¥–æ 30–∫–ì—Ü?
–í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö
WiseLord
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–î–æ–±–∞–≤–ª–µ–Ω–æ: –ß—Ç —è–Ω–≤ 05, 2017 14:03:55
–î—Ä—É–≥ –ö–æ—Ç–∞
–ö–∞—Ä–º–∞: 86
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 1035
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç –∞–ø—Ä 11, 2013 11:19:59–°–æ–æ–±—â–µ–Ω–∏–π: 4895–û—Ç–∫—É–¥–∞: –ú–∏–Ω—Å–∫
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 1
–î–∞. –ù–æ –ø–µ—Ä–µ–¥ —ç—Ç–∏–º –Ω—É–∂–Ω–æ –æ—Ç—Ñ–∏–ª—å—Ç—Ä–æ–≤–∞—Ç—å —á–∞—Å—Ç–æ—Ç—ã –≤—ã—à–µ 15, —á—Ç–æ–±—ã –∏—Ö –Ω–∞ –≤—Ö–æ–¥–µ –∏ –Ω–µ –ø–æ—è–≤–ª—è–ª–æ—Å—å. –ò–Ω–∞—á–µ 16–∫–ì—Ü –±—É–¥–µ—Ç –æ—Ç–æ–±—Ä–∞–∂–∞—Ç—å—Å—è –≤ 14–∫–ì—Ü, 20–∫–ì—Ü –±—É–¥–µ—Ç –≤–∏–¥–Ω–æ –∫–∞–∫ 10–∫–ì—Ü –∏ —Ç.–¥.
–í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö
NebelWefer
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–î–æ–±–∞–≤–ª–µ–Ω–æ: –ß—Ç —è–Ω–≤ 05, 2017 14:24:35
–ì—Ä—ã–∑–µ—Ç –∫–∞–Ω–∏—Ñ–æ–ª—å
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç –∞–ø—Ä 16, 2009 14:23:59–°–æ–æ–±—â–µ–Ω–∏–π: 274
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
–ê–∞–∞, —è—Å–Ω–æ, –∏–Ω—ã–º–∏ —Å–ª–æ–≤–∞–º–∏, —á–∞—Å—Ç–æ—Ç–∞ –¥–∏—Å–∫—Ä–µ—Ç–∏–∑–∞—Ü–∏–∏ –í–°–ï–ì–î–ê –¥–æ–ª–∂–Ω–∞ –≤—ã—á–∏—Å–ª—è—Ç—å—Å—è –∏–∑ –º–∞–∫—Å–∏–º–∞–ª—å–Ω–æ–π —á–∞—Å—Ç–æ—Ç—ã —Å–∏–≥–Ω–∞–ª–∞, –Ω–µ–∑–∞–≤–∏—Å–∏–º–æ –æ—Ç –ø–æ—Ç—Ä–µ–±–Ω–æ—Å—Ç–µ–π. –°–ø–∞—Å–∏–±–æ –∑–∞ –ø–æ—è—Å–Ω–µ–Ω–∏–µ!
–ü–æ—Å–ª–µ –ø—Ä–æ—á—Ç–µ–Ω–∏—è —Ç–µ–º—ã –≤–æ–∑–Ω–∏–∫–ª–∞ –º—ã—Å–ª—å, —á—Ç–æ –Ω–µ –æ–±—è–∑–∞—Ç–µ–ª—å–Ω–æ –ø–æ–ª—É—á–∞—Ç—å –≤–µ—Å—å –º–∞—Å—Å–∏–≤ –∞–º–ø–ª–∏—Ç—É–¥ —á–∞—Å—Ç–æ—Ç –Ω–∞ –≤—ã—Ö–æ–¥–µ.
–¢–æ –µ—Å—Ç—å:
–ü–æ–ª—É—á–∏–ª–∏ –º–∞—Å—Å–∏–≤—ã RE –∏ IM, –∑–∞—Ç–µ–º —Ç–æ–ª—å–∫–æ –±–µ—Ä–µ–º —Ç–æ–ª—å–∫–æ —Ç–µ k , –∫–æ—Ç–æ—Ä—ã–µ —Å–æ–æ—Ç–≤–µ—Ç—Å—Ç–≤—É—é –Ω—É–∂–Ω—ã–º —á–∞—Å—Ç–æ—Ç–∞–º, –∏—Å—Ö–æ–¥—è –∏–∑ –ø—Ä–∏–º–µ—Ä–∞ —Ç–æ–≤–∞—Ä–∏—â–∞
Jordan `–∞
jordan –ø–∏—Å–∞–ª(–∞):
–ö–æ–¥:
for (int k = 0; k < 1024; k++)
–ï—Å–ª–∏ –º–Ω–µ –Ω—É–∂–Ω—ã –∞–º–ø–ª–∏—Ç—É–¥—ã, –Ω–∞–ø—Ä–∏–º–µ—Ä 1–∫–ì—Ü –∏ 5–∫–ì—Ü, —Ç–æ —è –≤—ã–±—Ä–∞—Å—ã–≤–∞—é –≤–µ—Ä—Ö–Ω–∏–π —Ü–∏–∫–ª –∏ –æ—Ç–¥–µ–ª—å–Ω–æ —Å—á–∏—Ç–∞—é –¥–ª—è k=(f–≥–∞—Ä–º * SIZE) / f–¥–∏—Å–∫—Ä.
–∫1=1000*1024/40000= 25 –∏–ª–∏ 26,
–∫2=5000*1024/40000= 128
–í–µ—Ä–Ω–æ –ª–∏ —è –≤—ã–≤–µ–ª?
–í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö
–ö–Ý–ê–ú
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–î–æ–±–∞–≤–ª–µ–Ω–æ: –ß—Ç —è–Ω–≤ 05, 2017 15:10:52
–î—Ä—É–≥ –ö–æ—Ç–∞
–ö–∞—Ä–º–∞: 139
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 2918
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç —è–Ω–≤ 10, 2008 22:01:02–°–æ–æ–±—â–µ–Ω–∏–π: 24611–û—Ç–∫—É–¥–∞: –ú–æ—Å–∫–æ–≤—Å–∫–∞—è –æ–±–ª–∞—Å—Ç—å, –§—Ä—è–∑–∏–Ω–æ
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 1
–î–ª—è –ø–æ–ª—É—á–µ–Ω–∏—è –Ω–µ—Å–∫–æ–ª—å–∫–∏—Ö –≥–∞—Ä–º–æ–Ω–∏–∫ –Ω–µ –Ω—É–∂–Ω–æ –¥–µ–ª–∞—Ç—å –ë–ü–§. –î–ü–§ –≤ —Ç–∞–∫–æ–º —Å–ª—É—á–∞–µ —ç–∫–æ–Ω–æ–º–∏—á–Ω–µ–µ.
–í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö
NebelWefer
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± —è–Ω–≤ 14, 2017 10:43:44
–ì—Ä—ã–∑–µ—Ç –∫–∞–Ω–∏—Ñ–æ–ª—å
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç –∞–ø—Ä 16, 2009 14:23:59–°–æ–æ–±—â–µ–Ω–∏–π: 274
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
NebelWefer –ø–∏—Å–∞–ª(–∞):
–ï—Å–ª–∏ –º–Ω–µ –Ω—É–∂–Ω—ã –∞–º–ø–ª–∏—Ç—É–¥—ã, –Ω–∞–ø—Ä–∏–º–µ—Ä 1–∫–ì—Ü –∏ 5–∫–ì—Ü, —Ç–æ —è –≤—ã–±—Ä–∞—Å—ã–≤–∞—é –≤–µ—Ä—Ö–Ω–∏–π —Ü–∏–∫–ª –∏ –æ—Ç–¥–µ–ª—å–Ω–æ —Å—á–∏—Ç–∞—é –¥–ª—è k=(f–≥–∞—Ä–º * SIZE) / f–¥–∏—Å–∫—Ä.
–ü–æ–ª—É—á–∞–µ—Ç—Å—è –≤–µ—Ä–Ω–æ)
–Ý–µ–∞–ª–∏–∑–æ–≤–∞–ª —ç—Ç–æ—Ç –∫–æ–¥ "–≤ –ª–æ–±", —Ä–∞–±–æ—Ç–∞–µ—Ç, —á–∞—Å—Ç–æ—Ç—ã –≤—ã–¥–µ–ª—è—é—Ç—Å—è. –¢–µ–ø–µ—Ä—å –¥–µ–ª–æ —Ç–æ–ª—å–∫–æ –∑–∞ –æ–ø—Ç–∏–º–∏–∑–∞—Ü–∏–µ–π.
–ù–æ —Ö–æ—Ç–µ–ª–æ—Å—å –±—ã –µ—â–µ —É—Ç–æ—á–Ω–∏—Ç—å –ø–æ –≤—ã–±–æ—Ä—É —Ä–∞–∑–º–µ—Ä–∞ –º–∞—Å—Å–∏–≤–∞: –ø–æ–Ω—è—Ç–Ω–æ, —á—Ç–æ —á–µ–º –±–æ–ª—å—à–µ –º–∞—Å—Å–∏–≤, —Ç–µ–º –≤—ã—à–µ —Ä–∞–∑—Ä–µ—à–∞—é—â–∞—è —Å–ø–æ—Å–æ–±–Ω–æ—Å—Ç—å –ø–æ —á–∞—Å—Ç–æ—Ç–∞–º, –∞ –≤–æ—Ç –Ω–∞ —Ç–æ—á–Ω–æ—Å—Ç—å —Ä–µ–∑—É–ª—å—Ç–∞—Ç–∞ –≤–ª–∏—è–µ—Ç –ª–∏?
–ù–∞–ø—Ä–∏–º–µ—Ä, –µ—Å—Ç—å –º–∞—Å—Å–∏–≤—ã: 625 –ì—Ü, 1250, 1875... –∏ 312 625 937...
–û–¥–∏–Ω–∞–∫–æ–≤—ã–π —Ä–µ–∑—É–ª—å—Ç–∞—Ç –±—É–¥–µ—Ç –¥–ª—è 625 –ì—Ü? –ë—É–¥–µ—Ç –ª–∏ –≤–æ 2–º —Å–ª—É—á–∞–µ –≤–ª–∏—è–Ω–∏–µ —Å–æ—Å–µ–¥–Ω–∏—Ö —á–∞—Å—Ç–æ—Ç –º–µ–Ω—å—à–µ?
–í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö
–ö–Ý–ê–ú
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± —è–Ω–≤ 14, 2017 11:10:01
–î—Ä—É–≥ –ö–æ—Ç–∞
–ö–∞—Ä–º–∞: 139
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 2918
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç —è–Ω–≤ 10, 2008 22:01:02–°–æ–æ–±—â–µ–Ω–∏–π: 24611–û—Ç–∫—É–¥–∞: –ú–æ—Å–∫–æ–≤—Å–∫–∞—è –æ–±–ª–∞—Å—Ç—å, –§—Ä—è–∑–∏–Ω–æ
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
"–Ý–∞–∑—Ä–µ—à–∞—é—â–∞—è —Å–ø–æ—Å–æ–±–Ω–æ—Å—Ç—å –ø–æ —á–∞—Å—Ç–æ—Ç–∞–º" –≤–æ–æ–±—â–µ —Ç–æ –Ω–∞–∑—ã–≤–∞–µ—Ç—Å—è –ø–æ–ª–æ—Å–æ–π –∞–Ω–∞–ª–∏–∑–∞. –ò —ç—Ç–∞ –ø–æ–ª–æ—Å–∞ –æ–±—Ä–∞—Ç–Ω–æ –ø—Ä–æ–ø–æ—Ä—Ü–∏–æ–Ω–∞–ª—å–Ω–∞ –í–Ý–ï–ú–ï–ù–ò –ù–ê–ö–û–ü–õ–ï–ù–ò–Ø. –ê–ß–• —Ñ–∏–ª—å—Ç—Ä–∞ –ø—Ä–∏–≤–µ–¥–µ–Ω–Ω–∞—è –∫ –ø–æ–ª–æ—Å–µ –∞–Ω–∞–ª–∏–∑–∞ –≤—Å–µ–≥–¥–∞ –æ–¥–∏–Ω–∞–∫–æ–≤–∞. –ü–æ—ç—Ç–æ–º—É –∏–∑–±–∏—Ä–∞—Ç–µ–ª—å–Ω–æ—Å—Ç—å –ø–æ —Å–æ—Å–µ–¥–Ω–µ–º—É —Ñ–∏–ª—å—Ç—Ä—É –Ω–µ –∑–∞–≤–∏—Å–∏—Ç –æ—Ç —á–∏—Å–ª–∞ —Ñ–∏–ª—å—Ç—Ä–æ–≤. –ü—Ä–∏—á–µ–º –µ—Å–ª–∏ –±—ã –±—ã–ª–æ –∏–Ω–∞—á–µ, –ê–ß–• –∞–Ω–∞–ª–∏–∑–∞—Ç–æ—Ä–∞ –ø—Ä–µ–¥—Å—Ç–∞–≤–ª—è–ª–∞ —Å–æ–±–æ–π –≤–æ–ª–Ω–∏—Å—Ç—É—é –ª–∏–Ω–∏—é.
–í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö
NebelWefer
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± —è–Ω–≤ 14, 2017 14:01:50
–ì—Ä—ã–∑–µ—Ç –∫–∞–Ω–∏—Ñ–æ–ª—å
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç –∞–ø—Ä 16, 2009 14:23:59–°–æ–æ–±—â–µ–Ω–∏–π: 274
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
–ö–Ý–ê–ú –ø–∏—Å–∞–ª(–∞):
–≠–Ω–µ—Ä–≥–∏—è —Å–∏–≥–Ω–∞–ª–∞ –ø–æ–ø–∞–¥–∞—é—â–µ–≥–æ —Ä–æ–≤–Ω–æ –º–µ–∂–¥—É —Ñ–∏–ª—å—Ç—Ä–∞–º–∏ –ø–æ—Ä–æ–≤–Ω—É —Ä–∞—Å–ø—Ä–µ–¥–µ–ª–∏—Ç—Å—è –º–µ–∂–¥—É —ç—Ç–∏–º–∏ —Ñ–∏–ª—å—Ç—Ä–∞–º–∏.
–ü–æ–ª—É—á–∞–µ—Ç—Å—è –ø—Ä–∏ –±–æ–ª—å—à–µ–º –º–∞—Å—Å–∏–≤–µ —Ä–µ–∑—É–ª—å—Ç–∞—Ç —Ç–æ—á–Ω–µ–µ?
625 1250 1875
312 625 937 1250,
–µ—Å–ª–∏ –≤ —Å–∏–≥–Ω–∞–ª–µ –µ—Å—Ç—å —Å–æ—Å—Ç–∞–≤–ª—è—é—â–∞—è 900 –ì—Ü, —Ç–æ –≤ –ø–µ—Ä–≤–æ–º —Å–ª—É—á–∞–µ –µ–µ –ø—Ä–∏—Å—É—Ç—Å—Ç–≤–∏–µ –æ—Ç—Ä–∞–∑–∏—Ç—Å—è –∏ –Ω–∞ 625 –∏ –Ω–∞ 1250, –∞ –≤–æ 2–º —Å–ª—É—á–∞–µ –Ω–∞ 625 –∏ 937 –Ω–µ –ø–æ–ø–∞–≤ –≤ 1250.
–í–µ—Ä–Ω–æ?
–í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö
–ö–Ý–ê–ú
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–î–æ–±–∞–≤–ª–µ–Ω–æ: –°–± —è–Ω–≤ 14, 2017 14:14:41
–î—Ä—É–≥ –ö–æ—Ç–∞
–ö–∞—Ä–º–∞: 139
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 2918
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç —è–Ω–≤ 10, 2008 22:01:02–°–æ–æ–±—â–µ–Ω–∏–π: 24611–û—Ç–∫—É–¥–∞: –ú–æ—Å–∫–æ–≤—Å–∫–∞—è –æ–±–ª–∞—Å—Ç—å, –§—Ä—è–∑–∏–Ω–æ
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 1
–ï—Å—Ç–µ—Å—Ç–≤–µ–Ω–Ω–æ, —á–µ–º —É –∂–µ –ø–æ–ª–æ—Å–∞ –∞–Ω–∞–ª–∏–∑–∞, —Ç–µ–º —Ç–æ—á–Ω–µ–µ –º–æ–∂–Ω–æ –æ–ø—Ä–µ–¥–µ–ª–∏—Ç—å —Å–ø–µ–∫—Ç—Ä–∞–ª—å–Ω—ã–π –º–∞–∫—Å–∏–º—É–º —Å–∏–≥–Ω–∞–ª–∞. –ù–æ –ø—Ä–∏ —ç—Ç–æ–º –Ω–∞–¥–æ –ø–æ–Ω–∏–º–∞—Ç—å, —á—Ç–æ —Ä–µ–∞–ª—å–Ω—ã–µ —Å–∏–≥–Ω–∞–ª—ã –∏–º–µ—é—Ç –¥–æ—Å—Ç–∞—Ç–æ—á–Ω–æ —Ä–∞–∑–º—ã—Ç—ã–π —Å–ø–µ–∫—Ç—Ä, —Ö–æ—Ç—è –±—ã –≤ —Å–∏–ª—É –∏—Ö –æ–≥—Ä–∞–Ω–∏—á–µ–Ω–Ω–æ—Å—Ç–∏ –≤–æ –≤—Ä–µ–º–µ–Ω–∏. –¢–æ –µ—Å—Ç—å —É –∫–æ—Ä–æ—Ç–∫–æ–≥–æ –≤–æ –≤—Ä–µ–º–µ–Ω–∏ —Å–∏–≥–Ω–∞–ª–∞ –Ω–µ –º–æ–∂–µ—Ç –±—ã—Ç—å —É–∑–∫–æ–≥–æ —Å–ø–µ–∫—Ç—Ä–∞. –ê —Å—Ç—Ä–æ–≥–æ –º–æ–Ω–æ—Ö—Ä–æ–º–∞—Ç–∏—á–µ—Å–∫–∏–π —Å–ø–µ–∫—Ç—Ä –∏–º–µ–µ—Ç –±–µ—Å–∫–æ–Ω–µ—á–Ω–∞—è –≤–æ –≤—Ä–µ–º–µ–Ω–∏ —Å–∏–Ω—É—Å–æ–∏–¥–∞. –°–∏—Ä–µ—á—å, –ù–ò–ö–ê–ö–ê–Ø —Ä–µ–∞–ª—å–Ω–∞—è —Å–∏–Ω—É—Å–æ–∏–¥–∞ –Ω–µ –º–æ–∂–µ—Ç –±—ã—Ç—å —Å—Ç—Ä–æ–≥–æ –º–æ–Ω–æ—Ö—Ä–æ–º–∞—Ç–∏—á–Ω–æ–π.
–í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö
NebelWefer
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–î–æ–±–∞–≤–ª–µ–Ω–æ: –í—Å —è–Ω–≤ 15, 2017 18:05:20
–ì—Ä—ã–∑–µ—Ç –∫–∞–Ω–∏—Ñ–æ–ª—å
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç –∞–ø—Ä 16, 2009 14:23:59–°–æ–æ–±—â–µ–Ω–∏–π: 274
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 0
–ü—Ä–µ–¥–ª–∞–≥–∞—é –µ—â–µ –Ω–µ–º–Ω–æ–≥–æ —Ä–∞–∑–≤–∏—Ç—å —Ç–µ–º—É –¥–ª—è –ø–æ–ª–Ω–æ—Ç—ã –∫–∞—Ä—Ç–∏–Ω—ã. –í–µ–∑–¥–µ —É–ø–æ–º–∏–Ω–∞—é—Ç—Å—è —Ç–∞–±–ª–∏—Ü—ã sin/cos –¥–ª—è —É—Å–∫–æ—Ä–µ–Ω–∏—è –≤—ã—á–∏—Å–ª–µ–Ω–∏–π. –Ø –ø–æ–ø—Ä–æ–±–æ–≤–∞–ª —Ç–∞–∫: —Ä–∞—Å—Å—á–∏—Ç–∞–ª –≤ —ç–∫—Å–µ–ª–µ –¥–ª—è K=1, –≤ –ø—Ä–æ–µ–∫—Ç –¥–æ–±–∞–≤–∏–ª –º–∞—Å—Å–∏–≤, —É–º–Ω–æ–∂–µ–Ω–Ω—ã–π –Ω–∞ 10000:
–ö–æ–¥:
const short sin_k1[N] = {10000, 9998 .......}
—Ç–µ–ø–µ—Ä—å –∫—É—Å–æ–∫:
–ö–æ–¥:
x_real[k] += x_n[n] * Math.Cos( (-2) * Math.PI * k * n / 1024 );
—Å—Ç–∞–ª –ø—Ä–æ—Å—Ç–æ:
–ö–æ–¥:
x_real[k] += x_n[n] *sin_k1[n]/10000
—Ä–∞–±–æ—Ç–∞–µ—Ç –¥–µ–π—Å—Ç–≤–∏—Ç–µ–ª—å–Ω–æ –±—ã—Å—Ç—Ä–µ–µ, –Ω–æ –Ω–∞ —Ç–∞–∫–æ–π –º–∞—Å—Å–∏–≤ —É—Ö–æ–¥–∏—Ç –∫—É—á–∞ –ø–∞–º—è—Ç–∏, –∞ –µ—â–µ –∏ –¥–ª—è –¥—Ä—É–≥–∏—Ö –ö –Ω—É–∂–Ω—ã.
–ö–∞–∫ –≤—ã –æ–±—Ö–æ–¥–∏—Ç–µ —ç—Ç–æ—Ç –º–æ–º–µ–Ω—Ç?
–í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö
–ö–Ý–ê–ú
–ó–∞–≥–æ–ª–æ–≤–æ–∫ —Å–æ–æ–±—â–µ–Ω–∏—è: Re: FFT –Ω–∞ –°–∏ –¥–ª—è AVR
–î–æ–±–∞–≤–ª–µ–Ω–æ: –í—Å —è–Ω–≤ 15, 2017 19:09:20
–î—Ä—É–≥ –ö–æ—Ç–∞
–ö–∞—Ä–º–∞: 139
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏–π: 2918
–ó–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω: –ß—Ç —è–Ω–≤ 10, 2008 22:01:02–°–æ–æ–±—â–µ–Ω–∏–π: 24611–û—Ç–∫—É–¥–∞: –ú–æ—Å–∫–æ–≤—Å–∫–∞—è –æ–±–ª–∞—Å—Ç—å, –§—Ä—è–∑–∏–Ω–æ
–Ý–µ–π—Ç–∏–Ω–≥ —Å–æ–æ–±—â–µ–Ω–∏—è: 1
–õ—é–±–∞—è —Ç–∞–±–ª–∏—Ü–∞, –∞ –æ—Å–æ–±–µ–Ω–Ω–æ –±–æ–ª—å—à–∞—è, –¥–æ–ª–∂–Ω–∞ —Ä–∞–∑–º–µ—â–∞—Ç—å—Å—è –≤ –ø—Ä–æ–≥—Ä–∞–º–º–Ω–æ–º —Ñ–¥–µ—à–µ. –ê –ú–ö –∑–∞—Ç–æ—á–µ–Ω–Ω—ã–µ, –≤ —Ç–æ–º —á–∏—Å–ª–µ, –ø–æ–¥ –ø—Ä–∏–º–µ–Ω–µ–Ω–∏–µ —Ç–∞–±–ª–∏—Ü –¥–æ–ª–∂–Ω—ã –∏–º–µ—Ç—å –∏–Ω—Å—Ç—Ä—É–º–µ–Ω—Ç –±—ã—Å—Ç—Ä–æ–π –≤—ã–±–æ—Ä–∫–∏ –¥–∞–Ω–Ω—ã—Ö –∏–∑ —Ñ–ª–µ—à–∞, –¥–ª—è —á–µ–≥–æ –æ–±–ª–∞—Å—Ç—å —Ñ–ª–µ—à–∞ —Ç–∞–∫ –∏–ª–∏ –∏–Ω–∞—á–µ –æ—Ç—Ä–∞–∂–µ–Ω–∞ –≤ –∞–¥—Ä–µ—Å–Ω–æ–µ –ø—Ä–æ—Å—Ç—Ä–∞–Ω—Å—Ç–≤–æ –û–ó–£.
–í–µ—Ä–Ω—É—Ç—å—Å—è –Ω–∞–≤–µ—Ä—Ö
–°—Ç—Ä–∞–Ω–∏—Ü–∞ 6 –∏–∑ 10
[ –°–æ–æ–±—â–µ–Ω–∏–π: 200 ]
... , , , , , , ,
–ö—Ç–æ —Å–µ–π—á–∞—Å –Ω–∞ —Ñ–æ—Ä—É–º–µ
–°–µ–π—á–∞—Å —ç—Ç–æ—Ç —Ñ–æ—Ä—É–º –ø—Ä–æ—Å–º–∞—Ç—Ä–∏–≤–∞—é—Ç: –Ω–µ—Ç –∑–∞—Ä–µ–≥–∏—Å—Ç—Ä–∏—Ä–æ–≤–∞–Ω–Ω—ã—Ö –ø–æ–ª—å–∑–æ–≤–∞—Ç–µ–ª–µ–π –∏ –≥–æ—Å—Ç–∏: 25
–í—ã –Ω–µ –º–æ–∂–µ—Ç–µ –Ω–∞—á–∏–Ω–∞—Ç—å —Ç–µ–º—ã–Ω–µ –º–æ–∂–µ—Ç–µ –æ—Ç–≤–µ—á–∞—Ç—å –Ω–∞ —Å–æ–æ–±—â–µ–Ω–∏—è–Ω–µ –º–æ–∂–µ—Ç–µ —Ä–µ–¥–∞–∫—Ç–∏—Ä–æ–≤–∞—Ç—å —Å–≤–æ–∏ —Å–æ–æ–±—â–µ–Ω–∏—è–Ω–µ –º–æ–∂–µ—Ç–µ —É–¥–∞–ª—è—Ç—å —Å–≤–æ–∏ —Å–æ–æ–±—â–µ–Ω–∏—è–Ω–µ –º–æ–∂–µ—Ç–µ –¥–æ–±–∞–≤–ª—è—Ç—å –≤–ª–æ–∂–µ–Ω–∏—è

































 –ù–æ –≥–¥–µ –∂–µ –æ–Ω–∞?
–ù–æ –≥–¥–µ –∂–µ –æ–Ω–∞? 